Vocalises sérielles : Séries dodécaphoniques cycliques
André Papillon
Université Laval
Résumé
Préambule
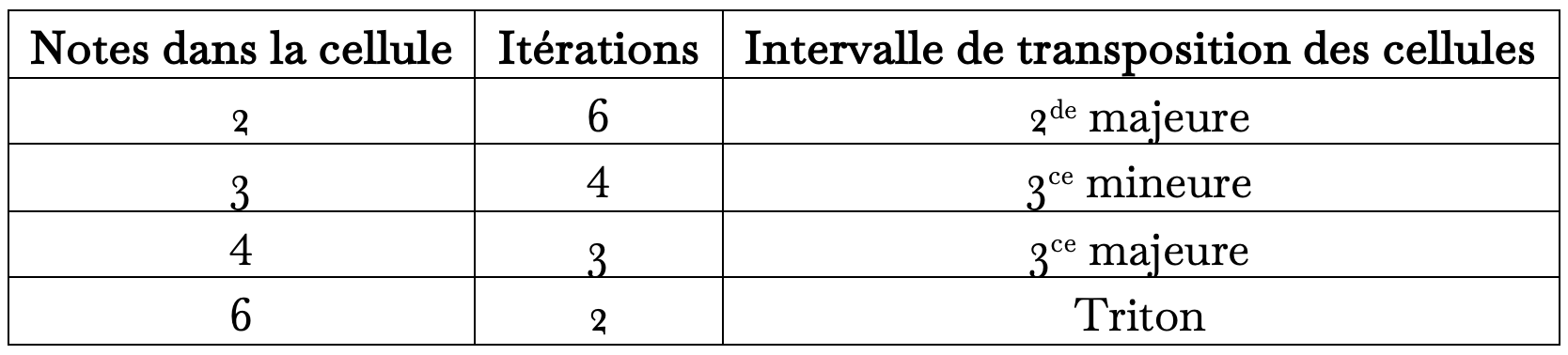
Quoique cet essai porte sur des séries dodécaphoniques, il n’y sera aucunement question de théories sérielles, de techniques de composition, voire de musique! Il s’agit tout simplement de la réponse à une question de nature essentiellement mathématique : combien existe-t-il de séquences répétitives de 2, 3, 4 ou 6 intervalles qui couvrent, en douze notes, le total chromatique?
Cette même question aurait pu être explorée sans référence musicale avec cette variante : Si, à partir de midi–minuit sur un cadran d’horloge, on avance l’aiguille de trois heures pour ensuite la reculer d’une heure, et que ces deux opérations consécutives sont répétées 5 fois, l’aiguille se retrouve au point de départ et chaque opération aura mené le curseur à une heure différente : 12–3–2–5–4–7–6–9–8–11–10–1–12.
Combien existe-t-il de séquences répétées de deux sauts qui ont cette caractéristique de ramener le curseur au point de départ sans repasser par la même heure? La même question peut être posée avec des séquences de trois, quatre et six sauts.
Introduction
Tous les musiciens occidentaux connaissent au moins deux séries dodécaphoniques : la gamme chromatique et le cycle des quintes. Ces deux séries ont également en commun le fait d’être basées sur un seul intervalle répété 12 fois.
Peut-on imaginer des séries dodécaphoniques basées sur l’alternance de deux intervalles? Il y en a deux : la première est basée sur l’alternance entre une 3ce mineure et une 2de mineure en mouvements contraires, et la seconde, sur l’alternance entre une 4te juste et une 3ce mineure en mouvements contraires :
On peut se poser la même question avec des séquences répétées de trois, quatre et six intervalles1. Cet essai porte sur ces séries, les méthodes pour les découvrir et certaines de leurs caractéristiques.
Abréviations
SP Série périodique
SP2 Série périodique basée sur une cellule de 2 notes. Idem pour SP3, SP4 et SP6.
Séries périodiques
Une série périodique sérielle est une séquence de 2, 3, 4 ou 6 intervalles, jouée en boucle et qui génère à la 12e note une série dodécaphonique.
Elle peut prendre quatre formes :
Une séquence de 2 notes, répétée un ton plus haut ou plus bas (SP2) :
Une séquence de 3 notes, répétée une 3ce mineure plus haut ou plus bas (SP3) :
Une séquence de 4 notes, répétée une 3ce majeure plus haut ou plus bas (SP4) :
Une séquence de 6 notes, répétée à un triton de distance2 (SP6) :
Transposition limitée
En principe, une série peut être notée dans 12 transpositions. Toutefois, les séries qui font l’objet de cette étude sont à transposition limitée : le nombre de transpositions correspond au nombre de notes dans la cellule de base.
Prenons par exemple cette série basée sur une cellule de deux notes :
Elle peut être transposée un demi-ton plus haut :
Si on la transpose un autre demi-ton plus haut, on retrouve la série originelle, avec une translation (dans cet exemple, la série originelle débute par la 3e note et se termine par les deux premières).
Translation limitée
En principe, une série peut commencer par n’importe laquelle de ses 12 notes. Toutefois, les séries qui font l’objet de cette étude sont à translation limitée : le nombre de translations correspond également au nombre de notes dans la cellule de base.
Prenons par exemple cette série :
Elle peut être décalée d’une note :
Si on la décale une autre fois, on y retrouve la série d’origine, un ton plus haut :
Quelle que soit la transposition ou la translation de ces séries, elles sont basées sur une même séquence d’intervalles qui servira d’identifiant unique.
Notation des intervalles et des séries périodiques
Les séries sont plus aisément reconnaissables dans toutes leurs transpositions et translations lorsqu’on les traite comme des séquences d’intervalles plutôt que des séquences de notes.
Prenons par exemple cette série :
Elle est composée d’une variété d’intervalles : 7es majeures et 8ves diminuées descendantes, 8ves augmentées et 9es mineures ascendantes.
Puisqu’une série dodécaphonique est une suite de hauteurs nominales3, on peut modifier les registres des notes par des sauts d’octaves afin de les ramener au plus petit intervalle avec la note précédente. On constate alors qu’il s’agit tout simplement d’une gamme chromatique ascendante :
Ces intervalles peuvent donc être identifiés par un même signe qui identifierait également les intervalles disjoints de l’exemple précédent. Les nombres utilisés dans la théorie sérielle étant parfois utilisés pour identifier des notes ou des intervalles sans égard à la direction, j’ai choisi d’utiliser les onze premières lettres de l’alphabet pour éviter toute équivoque.
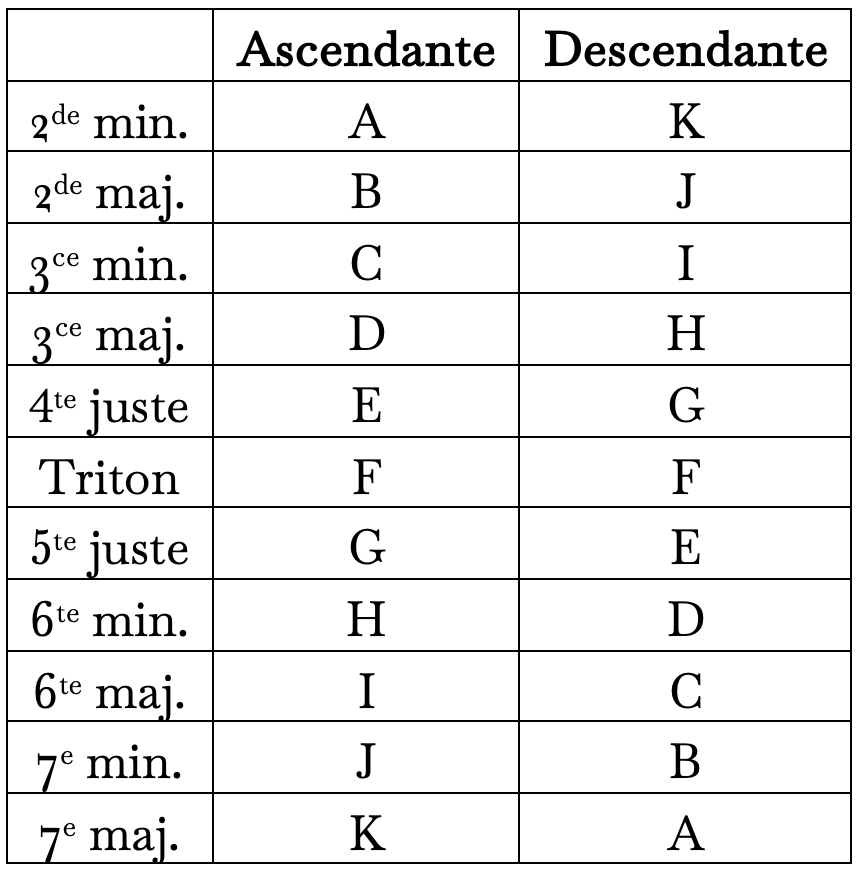
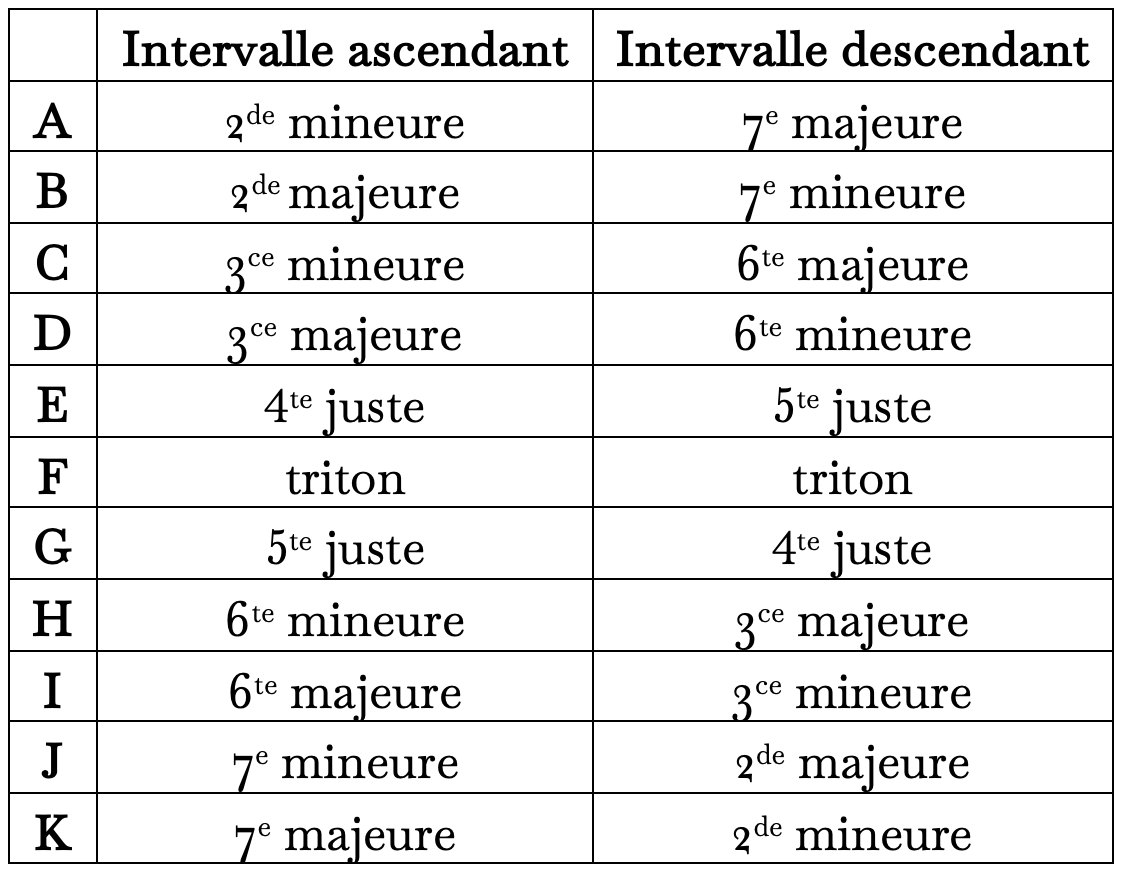
On observe qu’une même lettre peut identifier un intervalle et son renversement, c’est-à-dire des intervalles complémentaires.
Inversion ou renversement?
Avant d’aller plus loin, il est important de bien distinguer l’inversion et le renversement.
Renversement : les mêmes notes dans des mouvements contraires forment deux intervalles complémentaires, c’est-à-dire que leur somme est égale à une octave4. Dans notre notation alphabétique des intervalles, le même identifiant décrit deux intervalles complémentaires :
Inversion : Le même intervalle en mouvement contraire.
Autrement dit :

Identifiant unique
Contrairement à une mélodie qui est une suite fixe d’intervalles avec un début et une fin, une série est une séquence circulaire d’intervalles. La première note ou le premier intervalle utilisé dans une série ne lui donne aucune importance particulière.
Comme une série peut prendre jusqu’à 144 formes différentes (12 translations multipliées par 12 transpositions), ces doublons sont très fréquents et leur détection s’avère laborieuse.
Pour repérer plus facilement les doublons, on convient d’un identifiant unique dont la première lettre est la plus proche du début de l’alphabet.
Par exemple, GBACDE commencera par A, donc ACDE, suivi des lettres qui précèdent A, c’est-à-dire GB : ACDEGB. Si une lettre est doublée, on choisit celle qui est suivie de la lettre la plus proche du début de l’alphabet : GBDBCE sera donc BCEGBD.
Matrice de Schoenberg
Une autre manière de trouver d’autres séries à partir d’une série donnée est d’utiliser la matrice de Schoenberg qui génère le rétrograde, l’inversion et l’inversion du rétrograde d’une série.
Dans cet exemple, le rétrograde (R) de DAJ génère KHB :
Dans cet exemple, l’inversion (I) de DAJ génère BHK :
On note que les identifiants du rétrograde et de l’inversion d’une même série sont des palindromes (dans cet exemple, KHB et BHK).
Dans cet exemple, l’inversion du rétrograde de DAJ génère la série JAD :
On note que l’identifiant d’une série et celui de l’inversion du rétrograde d’une série sont des palindromes.
Familles de séries
Dans l’annexe de cet essai, les séries sont regroupées par familles lorsqu’elles appartiennent à la même matrice de Schoenberg, c’est-à-dire une série P (prime5), son rétrograde (R), son inversion (I) et l’inversion du rétrograde (RI). Pour les SP qui sont des palindromes intervalliques6, R et I sont semblables, ainsi que P et RI.
Chaque série d’une même famille peut être considérée comme prime.
Comment trouver les séries périodiques?
Séries avec un seul intervalle
Il existe quatre intervalles qui génèrent des séries lorsqu’ils sont répétés 12 fois : le demi-ton (ascendant et descendant) et la quinte (ascendante et descendante). Les deux premiers intervalles génèrent les gammes chromatiques, les deux autres génèrent les cycles des quintes.
Cellules de deux notes
Puisque chaque cellule est transposée un ton plus haut ou plus bas, l’ensemble des premières notes de chaque cellule forme une gamme par tons (il en va de même pour les secondes notes).
Chaque note d’une cellule devant provenir d’une gamme par tons différente, les seuls intervalles possibles entre deux notes consécutives sont ceux qu’on ne retrouve pas dans une gamme par tons.

Comme chaque cellule est suivie de sa transposition un ton plus haut ou plus bas, il existe deux possibilités d’intervalles entre la seconde note d’une cellule et la première de la suivante.
Dans la figure ci-haut, les deux premières notes de chaque mesure représentent les notes d’une cellule, et la double note sur le 3e temps représente les deux possibilités de première note de la cellule suivante.
La 1re ligne de l’identifiant est associée à la séquence des notes avec les hampes ascendantes.
La 2e ligne de l’identifiant est associée à la séquence des notes avec les hampes descendantes.
Cette figure comprend les quatre séries à un seul intervalle : AA, EE, GG et KK.
Une modification dans l’ordre des notes d’une cellule génère une série différente :
Nous verrons plus loin que la modification de l’ordre des notes à l’intérieur d’une même cellule peut être utilisé comme un procédé pour générer d’autres séries.
On retrouve, dans la série périodique CK, la formule B-A-C-H, répétée une tierce majeure plus haut à deux reprises :
Cellules de trois notes
Combinaisons de base
L’ensemble des premières notes de chaque cellule forme un arpège de 7e diminuée (il en va de même pour les deuxièmes et troisièmes notes).
Puisque chaque note d’une cellule doit provenir d’un arpège de 7e diminuée différent, les cellules ne doivent pas contenir un des intervalles qui composent l’arpège de 7e diminuée, c’est-à-dire la 3ce mineure et le triton.
Voici les six combinaisons de trois notes qui ne contiennent aucune 3ce mineure et aucun triton :
Comme ces notes peuvent apparaître dans n’importe quel ordre à l’intérieur de la cellule, chaque groupe de trois notes représente six possibilités7 de combinaisons. À titre d’exemple, voici les séquences possibles de la combinaison E de la figure précédente :
Chacune des 6 permutations des 6 possibilités peut être suivi de sa transposition une tierce mineure plus haut ou plus bas, pour un potentiel de 6*6*2 = 72 possibilités. En éliminant les doublons, dont quatre qui appartiennent à la catégorie des séries basées sur un seul intervalle (A, E, G et K), il reste 24 séries regroupées en 8 familles.
Ce grand nombre de doublons s’explique notamment par le fait que presque toutes ces séries contiennent deux ou trois des six combinaisons de base.
Dans cet exemple, les trois groupes de notes en rouge avec hampes descendantes correspondent respectivement aux combinaisons D, C et E (voir page précédente) :
Groupes de quatre notes
Les premières notes des groupes de quatre notes formant un accord de quinte augmentée, les groupes ne peuvent pas contenir de 3ce majeure. Il existe huit ensembles distincts de quatre notes sans 3ce majeure :

Quatre de ces ensembles sont diatoniques (B, C, D, G). On retrouve également dans ces ensembles l’arpège de septième diminuée (H) ainsi qu'une suite chromatique (A).
Les SP générées par ces cellules ne sont pas mutuellement exclusives. Certaines SP contiennent deux ensembles :
À l’instar des groupes de 3 notes, les notes de ces formules peuvent se succéder dans n’importe quelle des 4! = 24 séquences possibles. Ces 8 ensembles avec leurs 24 permutations pouvant être suivies de leur répétition une 3ce majeure plus haut ou plus bas, nous trouvons 8*24*2 = 384 possibilités qui comprennent de nombreux doublons ainsi que des SP1 et SP2. Une exploration systématique nous a permis de distinguer 78 séries distinctes regroupées en 28 familles.
Groupes de six notes
L’intervalle de transposition des deux cellules de six notes qui forment les SP6 étant le triton, les cellules ne peuvent être formées que d’une de ces six combinaisons de six notes exemptes de tritons :
À l’instar des groupes de deux, trois et quatre notes, les notes de ces formules peuvent se succéder dans n’importe quelle des 6! = 720 séquences possibles.
Ces six ensembles avec leurs 720 permutations ne peuvent être suivies que de leur transposition un triton plus haut ou plus bas puisque les deux ont le même résultat. Ils génèrent donc 6*720 = 4 320 séquences possibles. Ces possibilités comprennent de nombreux doublons : une exploration systématique (et fastidieuse) nous a permis de distinguer 632 séries distinctes regroupées en 186 familles.
Particularités de certaines séries
Palindromes intervalliques
Certaines séquences d’intervalles sont palindromiques, ce qui toutefois ne signifie pas que les notes sont palindromiques (ce qui serait contradictoire avec la nature même d’une série dodécaphonique). Par exemple, le palindrome de BCKCBI est IBCKCB qui, ordonné, correspond à BCKCBI.
Un palindrome intervallique est semblable au rétrograde de son inversion (RI) et le rétrograde (R) d’un palindrome intervallique est semblable à son inversion (I)8.
C’est le cas notamment des séries basées sur des cellules de deux notes qui sont forcément des palindromes intervalliques : le palindrome de ABABAB est BABABA qui, ordonné, devient ABABAB.
Les identifiants de 6 des 8 (75%) familles de séries basées sur une cellule de 3 notes sont palindromiques.
Les identifiants de 17 des 28 (61%) familles de séries basées sur une cellule de 4 notes sont palindromiques.
Les identifiants de 53 des 184 (29%) familles de séries basées sur une cellule de 6 notes sont palindromiques.
Hexacordes diatoniques
Les six premières notes de la gamme majeure et leur répétition un triton plus haut forment une série :
La plupart des séries générées par les 6! = 720 permutations de ces hexacordes diatoniques en contiennent au moins un autre :
Dans cet exemple, les notes avec les hampes ascendantes consistent en un hexacorde diatonique suivi de sa transposition un triton plus haut. Les notes avec les hampes descendantes forment un hexacorde diatonique différent.
Certaines séries en génèrent davantage et il existe au moins une série qui contient cinq hexacordes diatoniques :
A : La série complète figure sur la 1re ligne et les autres hexacordes diatoniques qu’elle contient sont isolées dans les portées inférieures.
B : La série complète est reproduite sur toutes les lignes, mais transposée pour que l’hexacorde diatonique soit toujours composé des notes do – ré – mi – fa – sol – la.
On observe que le nombre d’intervalles disjoints dans un hexacorde diatonique est généralement proportionnel au nombre d’autres hexacordes diatoniques que la SP6 peut contenir. La SP6 basée sur l’hexacorde diatonique conjoint9 ne contient aucun autre hexacorde diatonique.
Tritonisation
Pour les fins de cet essai, la tritonisation est la transformation d’un intervalle lorsqu’une des notes qui le composent est transposée d’un triton, ou, par extension, la transformation d’une SP6 lorsqu’on remplace tous les intervalles par leur correspondant selon le tableau ci-dessous.
Dans une série basée sur une cellule de six notes, on peut échanger deux notes qui occupent la même position dans leurs cellules respectives sans affecter le caractère dodécaphonique de l’ensemble. Ces deux notes sont par définition à distance d’un triton puisque chaque note d’une SP6 est la transposition à un triton de distance de la note qui occupe la même position dans l’autre cellule.
Voici les intervalles qu’on peut retrouver dans une SP6 (c’est-à-dire tous sauf F) et leur transformation lorsqu’une note est transposée d’un triton :
Dans cet exemple, la lettre du haut est l’identifiant de l’intervalle formé par les notes avec les hampes ascendantes et la lettre inférieure est celui de l’intervalle formé par les notes avec les hampes descendantes.
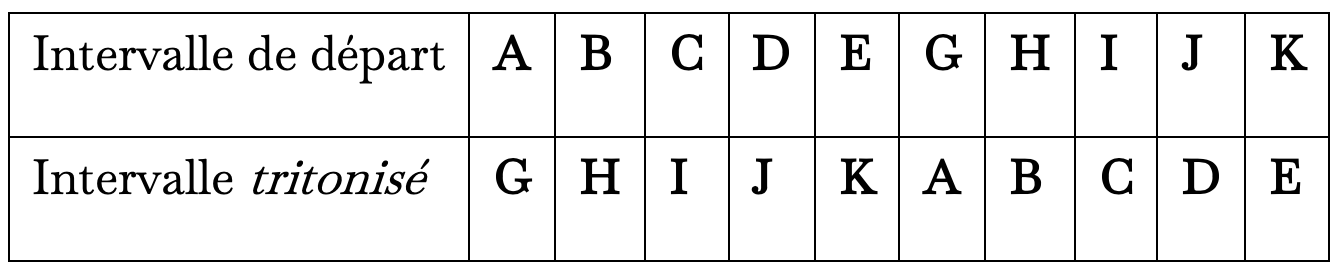
La transposition d’une seule note modifie les intervalles avec la note précédente et avec la suivante. Si on transpose deux notes consécutives, l’intervalle entre ces deux notes reste le même et seuls les intervalles avant et après cette nouvelle paire de notes sont modifiés.
Donc, si on alterne une note originale et une note transposée d’un triton, tous les intervalles seront modifiés. Or, on observe qu’en transposant d’un triton les notes impaires (1–3–5) ou les notes paires (2–4–6) d’une cellule, on génère la même SP6, à un triton de distance :
On peut donc en inférer qu’on peut générer de nouvelles SP6 en remplaçant toutes les lettres d’un identifiant selon cette correspondance biunivoque.
Ce qui rend cette opération possible est la commutativité de la correspondance entre les intervalles et leur tritonisation : la transposition au triton ascendant ou descendant génère la même note, ce qui n’est pas le cas des intervalles de transposition associés aux autres types de séries périodiques10. Un autre facteur contribue à expliquer cette particularité des SP6 : un triton reste un triton, quel que soit l’ordre des notes – le triton est sa propre inversion et son propre renversement.
En construisant la liste des 632 SP6, j’ai utilisé un outil en ligne de chiffrement11 pour générer en une seule opération un grand nombre de nouvelles SP à partir de leurs identifiants.
Séries auto-tritonisées
La tritonisation de certaines SP6 génère leur propre inversion. Ce premier exemple montre une série suivie de la transposition d’un triton d’une note sur deux (ici, les notes 1-3-5)12 :
L’exemple suivant montre la même série suivie de son inversion :
Ces deux opérations génèrent la même série : GJDKHB et KHBGJD qui, une fois ordonnés, donnent tous deux BGJDKH.
De même, l’inversion du rétrograde et la tritonisation du rétrograde de certaines série auto-tritonisées génèrent la même série. Au total, 15 des 184 familles de séries basées sur une cellule de 6 notes partagent cette caractéristique.
Conclusion
Une étude plus poussée pourrait se pencher sur les caractéristiques des séries auto-tritonisées et tenter d’expliquer pourquoi certaines séries possèdent cette caractéristique, plutôt que simplement le constater, comme je me suis contenté de le faire.
En tant que pédagogue instrumental, je considère que jouer et transposer une SP2 ou une SP3 peut présenter un certain intérêt pédagogique pour l’application des intervalles, mais une erreur dans une séquence atonale passe plus facilement inaperçue qu’une erreur dans un contexte tonal. Quant aux SP4-6, je considère que l’exercice fait principalement appel à la mémoire et au calcul mental. Ce sont, certes, des qualités indéniables dans tous les domaines d’activité, mais je crois qu’il y a des exercices plus constructifs et moins rébarbatifs pour les développer dans un contexte d’apprentissage musical. Je laisse aux chercheurs en pédagogie instrumentale le soin de décider si cette question mérite tout de même d’être étudiée.
- On ne peut exclure la possibilité que des séquences de x (≠ diviseur de 12) intervalles pourraient également générer des séries dodécaphoniques, mais elles laisseraient une séquence incomplète et perdraient leur caractère cyclique.↩︎
Plus haut ou plus bas, le résultat est le même.↩︎
Hauteur nominale, ou pitch class : note, sans égard à son registre.↩︎
La somme des intervalles qui composent une octave est 9 car la désignation des intervalles correspond à 1 + le nombre de degrés supplémentaires.↩︎
Comme j’utilise les initiales anglaises, j’utilise prime pour la correspondance avec l’initiale P.↩︎
Voir la section Palindromes intervalliques↩︎
Il y a 3! = 6 séquences possibles de trois notes abc : abc, acb, bac, bca, cab, cba↩︎
L’explication est dans la section Inversion ou renversement.↩︎
Voir le premier exemple de cette section.↩︎
2de majeure pour les SP2, 3ce mineure pour les SP3 et 3ce majeure pour les SP4.↩︎
La transposition des notes 2-4-6 génèrerait la même série à un triton de distance.↩︎
Musiques : Recherches interdisciplinaires 1, n°1